Global Lift

It's common for experiments to only impact a subset of the total audience (user base). In this case, a relevant question is "how will this localized experiment impact global metric values?". Eppo helps answer this question with its Global Impact calculator.

This page describes how experiment Global Lift and Coverage are calculated. For more information on using Global Lift, see this page in the experimental analysis documentation.

Computing global lift

To set the stage, let's consider the different populations of users throughout the experiment. First we note that for most real world experiments there is a population of users that are not eligible. This could be because they did not visit a certain page, or because they did not meet the targeting criteria for the experiment.

Next, we assume that there may be some users that are eligible for the experiment but still were not assigned to either variant. Examples include when an experiment has a traffic exposure less than 100%, or when experiments are run mutually exclusively to other concurrent experiment.

Note that this page will focus on an example where users are the experiment subject, but the same math also applies to AB tests ran on other subjects.

Formalizing counterfactuals

Now that we understand the difference populations, let's consider three scenarios:

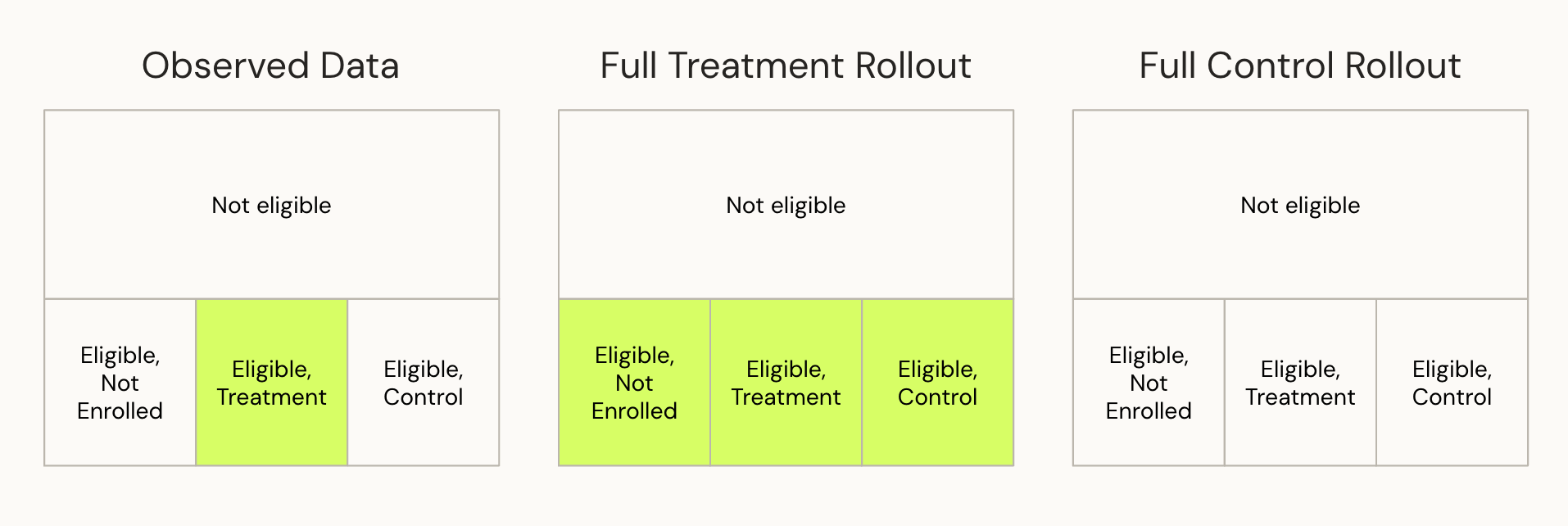
1. Observed Data: The scenario we actually observe: within the eligible population, the treatment group gets a new variant and both the control and "not enrolled" groups receive the baseline experience.
2. Full Treatment Rollout (FTR): The counterfactual scenario where the entire eligible population received treatment
3. Full Control Rollout (FCR): The counterfactual scenario where the entire eligible population received control

Visually, we can represent the different audiences and scenarios as follows:

A few definitions

We ultimately want to understand the relative lift between the two counterfactuals scenarios: $FTR$ and $FCR$. Let $TM_T$ and $TM_C$ represent the total metric value (across both eligible and ineligible users) for these two scenarios. Then, we can define Global Lift as

$$\Delta_{global} = \frac{TM_T - TM_C}{TM_C}$$

To measure this, let's first define a few more terms:

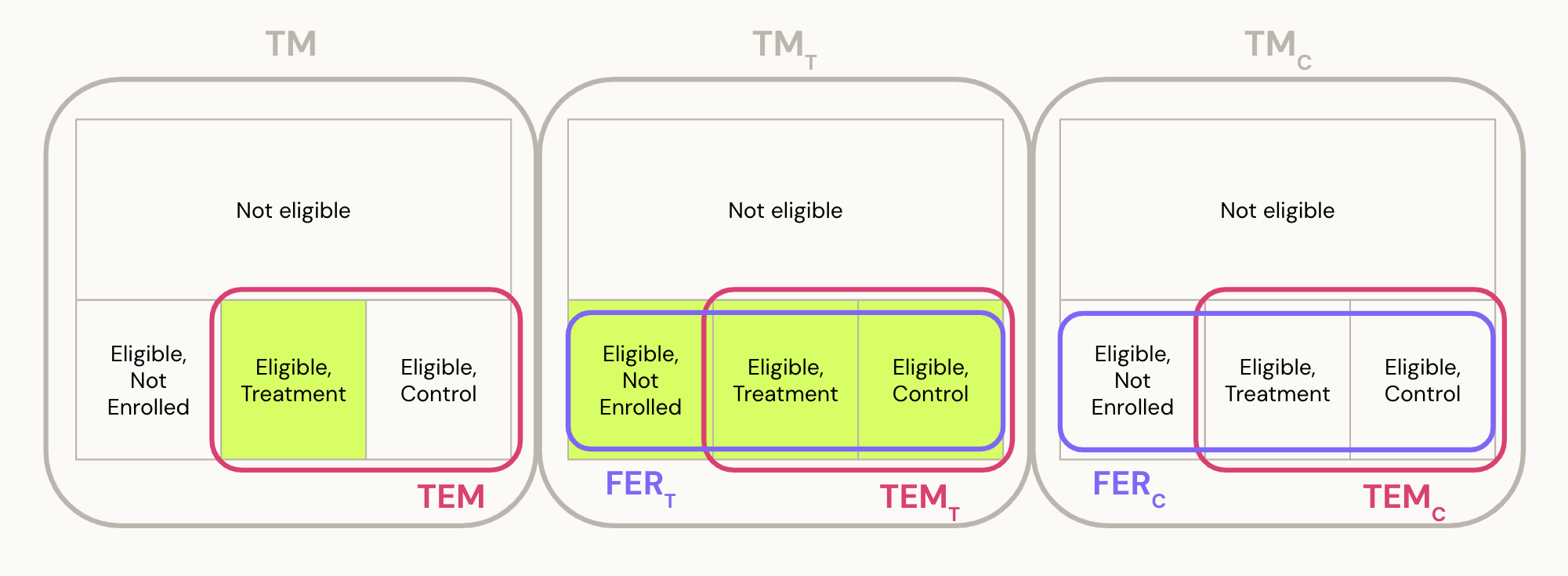
• $TM$ is the total metric value across all eligible and ineligible users in the observed data
• $X_T$ is the total metric value across users enrolled into treatment
• $X_C$ is the total metric value across users enrolled into control
• $TEM$ is the total metric value across eligible users enrolled into the experiment ($TEM= X_T + X_C$)
• $t_{exp}$ is the percent of eligible users randomly selected to be enrolled into the experiment
• $p_T$ is this percent of enrolled users who received the treatment (typically 50%)

All of these values can either be estimated directly from the observed data or are known from the experiment design. Next, we label similar terms in the other two scenarios. These are not directly observed and instead must be estimated from the values above.

• $TEM_T$ is the total metric value of enrolled users had they all received treatment
• $TEM_C$ is the total metric value of enrolled users had they all received control
• $FER_T$ is the total metric value for all eligible users had they received treatment (Full Experiment Rollout)
• $FER_C$ is the total metric value for all eligible users had they received control

Visually, we can represent all these terms as follows:

Deriving global lift

First note that since the ineligible population isn't impacted by rolling out the experiment,

$$TM_T - TM_C = FER_T - FER_C.$$

Next, $FER_C$ can be estimated by scaling $X_C$ to the full eligible audience:

$$FER_C = \frac{TEM_C}{t_{exp}} = \frac{1}{t_{exp}} \cdot \frac{X_C}{1 - p_T}.$$

Similarly, $FER_T$ is given by

$$FER_T = \frac{1}{t_{exp}} \cdot \frac{X_T}{p_T}.$$

We now know how to compute $TM_T - TM_C$. Next we compute $TM_C$ by itself. To do this we just need to subtract the lift from the experiment from the observed global metric value:

$$TM_C = TM - (TEM - TEM_C) = TM - \left(TEM - \frac{X_C}{1-p_T}\right)$$

Putting this all together, we have our final expression for Global Lift:

$$\Delta_{global} = \frac{TM_T - TM_C}{TM_C} = \frac{1}{t_{exp}} \left ( \frac{X_T}{p_T} - \frac{X_C}{1 - p_T} \right ) / \left (TM - TEM + \frac{X_C}{1-p_T} \right )$$

Coverage

In additional to Global Lift, Eppo also displays the Coverage of the experiment. This is simply the percentage of the global metric value that came from subjects in the experiment:

$$Coverage = TEM / TM.$$

Coverage is not used in the Global Lift calculation above, but instead indicates how much of the total population was included in a given experiment, weighted by the metric of interest.